El poder de interes compuesto

El poder del interés compuesto, es una fuerza a tener en cuenta. Invierte hoy, el dinero se multiplica en el futuro. La reinversión de los rendimientos, es un medio de crecimiento exponencial para tus ahorros. Imagínalo, tu dinero creciendo. Cuanto antes empieces, mayor será el potencial de crecimiento.
Interés Compuesto: Una definición
El interés compuesto es un sistema en el cual los intereses generados se añaden al capital principal, formando una base cada vez mayor sobre la cual se calcula el interés.
A diferencia del interés simple en el cual solo se calcula sobre el capital original, el interés compuesto permite ganar interés sobre los intereses acumulados. Esto da lugar a un crecimiento acelerado.
Un ejemplo de la diferencia entre interés simple y compuesto con un período de 2 años:
Supongamos que inviertes $1,000 a una tasa de interés del 10% anual.
Interés Simple:
- En el primer año, ganarías $100 en intereses ($1,000 x 10%) y tu inversión total sería de $1,100.
- En el segundo año, también ganarías $100 en intereses sobre el capital original de $1,000. Para un balance de $1,200.
Interés Compuesto:
- En el primer año, ganarías $100 en intereses ($1,000 x 10%) y el balance sería de $1,100.
- Sin embargo, en el segundo año, reinviertes los $100 de intereses generados el primer año. Ahora tu inversión total es de $1,100 en lugar de $1,000.
- En el segundo año, ganarías $110 en intereses ($1,100 x 10%) y tu balance sería de $1,210.
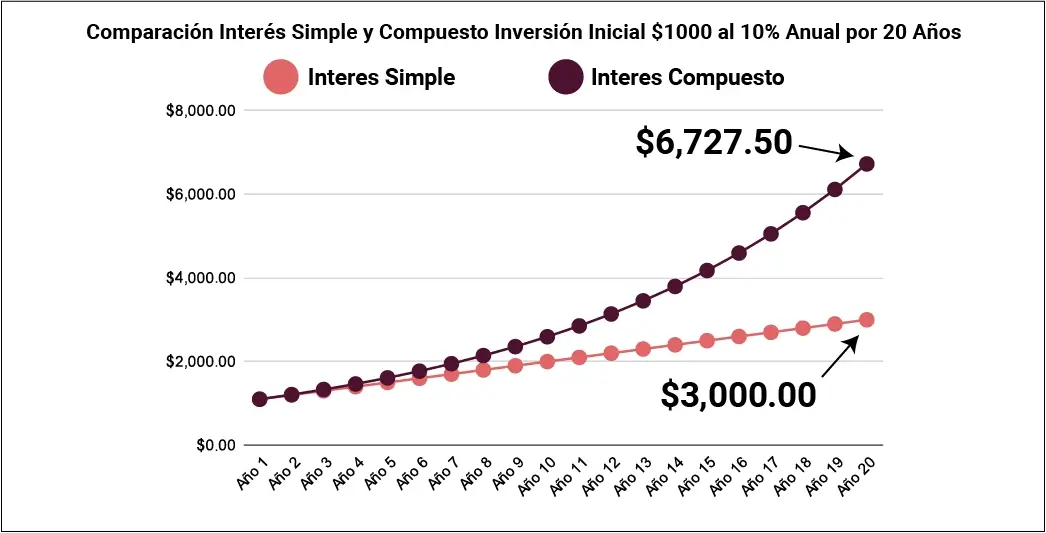
Como se puede ver en este ejemplo, a lo largo de dos años, el interés compuesto genera $10 en intereses adicionales en comparación con el interés simple. A medida que el período de inversión se alarga, la diferencia en los intereses generados entre ambos sistemas se vuelve cada vez mayor.
Formula de interes compuesto

La fórmula del interés compuesto es A = P(1 + (r/n))nt, donde (A) es el monto final, (P) es el capital inicial, (r) es la tasa de interés, (t) es el número años y (n) es el número de períodos de capitalización por año. Es importante saber cada una de estas variables para calcular el interés compuesto de manera precisa.
Ejemplo calculo de interés compuesto
Un ejemplo de interés compuesto con un período de 5 años, capitalizado mensualmente, un capital inicial de $100 y una tasa de interés del 5% anual:
- La fórmula para calcular el interés compuesto es: A = P(1 + (r/n))nt, donde A es el monto final, P es el capital inicial, r es la tasa de interés, n es el número de períodos de capitalizacion por años y t es el número de años.
- A = $100(1 + (0.05/12))(12*5) = $128.34 redondeado al centavo.
En este ejemplo se puede ver como aplicando la fórmula del interés compuesto se obtiene el monto final en un solo paso, en lugar de ir haciendo el cálculo año por año. El resultado es el mismo, pero el proceso es más sencillo.
Importancia del tiempo ( t )
Cuando eres joven, es posible que no pienses en la jubilación. Puede ser tentador ahorrar poco para el futuro y consumir más en el momento. Pero esto puede reducir seriamente la cantidad de dinero que tienes cuando te retires.
Una simple comparación ilustra el punto:
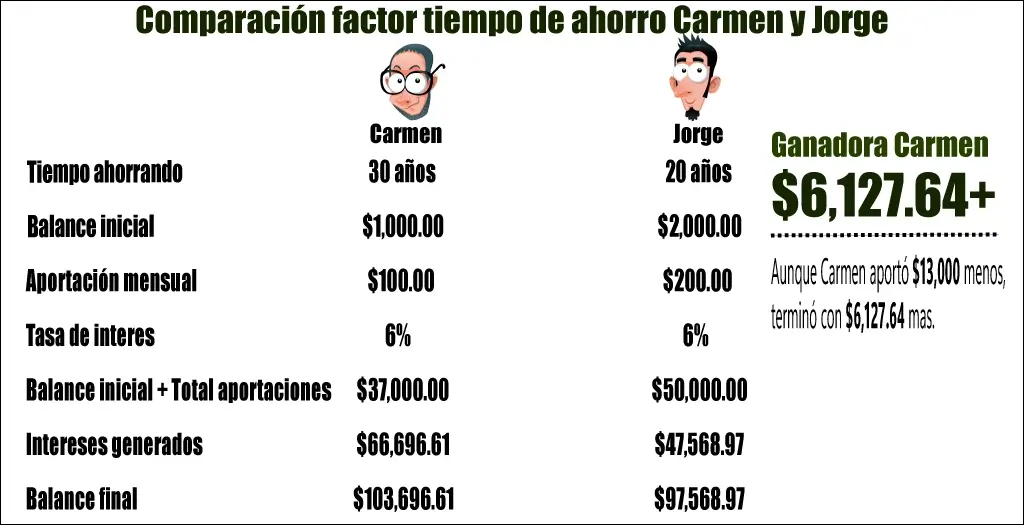
Jorge comienza a ahorrar a los 30 años, con un balance inicial de $2,000.00, aportando $200 mensuales por 20 años al 6% de interés que se capitaliza anualmente.
- Balance final $97,568.97
- Aportes + Balance inicial $50,000.00
- Intereses generados $47,568.97
Carmen comienza a ahorrar cuando tiene 20 años, con un balance inicial de $1,000.00, aportando $100 cada mes durante 30 años al 6% de interés que se capitaliza anualmente.
- Balance final $103,696.61
- Aportes + Balance Inicial $37,000.00
- Intereses Generados $66,696.61
Mientras que Jorge aportó $13,000.00 más que Carmen al retiro, terminó con $6,127.64 menos. La razón es el tiempo. Carmen comenzó a ahorrar 10 años antes y tuvo el beneficio de interés compuesto por un período más largo.
La lección es clara: cuanto antes empieces a ahorrar para la jubilación, mejor estarás.
Importancia de la tasa de interés ( r )
Cuanto mayor sea la tasa de interés de tus ahorros o inversiones, más dinero ganarás. Esto se debe a que una tasa de interés más alta significa que tu dinero crecerá más rápido. Incluso dos puntos porcentuales pueden marcar una gran diferencia con el tiempo. La relación es al revés si hablamos de dinero que hay que devolver. Cuanto menor sea la tasa de interés de un préstamo, mejor será para ti.
Veamos algunos números:
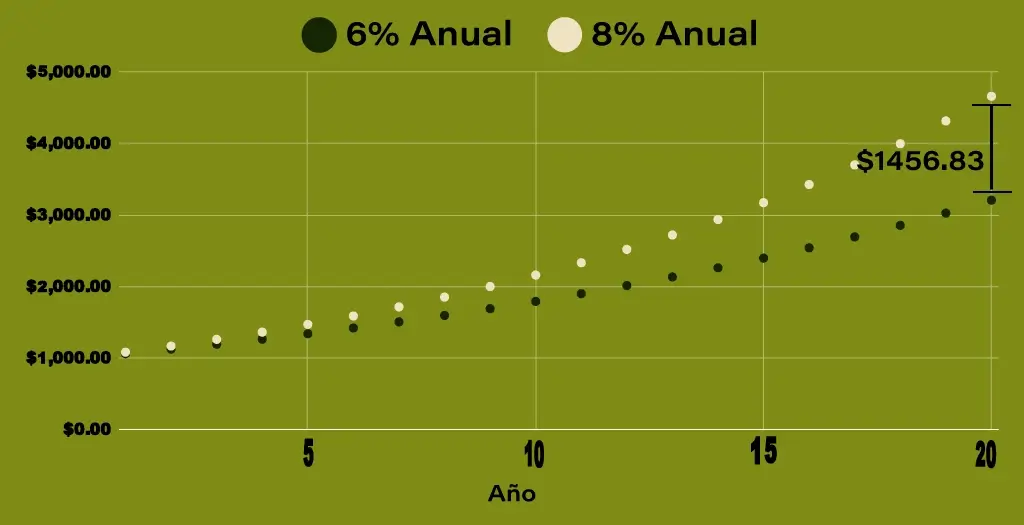
La diferencia entre una inversión de $1,000 al 8% o al 6% puede ser mucho dinero. Durante 20 años, sería $1456.83. Ambos ejemplos se capitalizan anualmente. Cuando hablamos de interés compuesto, la tasa de interés es de primera consideración.
Importancia de la frecuencia de capitalización ( n )
La capitalización es el proceso de generar ganancias sobre las ganancias reinvertidas de un activo. En otras palabras, es el interés sobre el interés. Cuanto más frecuentemente ocurra la capitalización, mayor será el efecto sobre el rendimiento total.
Una inversión de $ 1000 al 8% compuesto diariamente, versus anualmente durante 20 años:
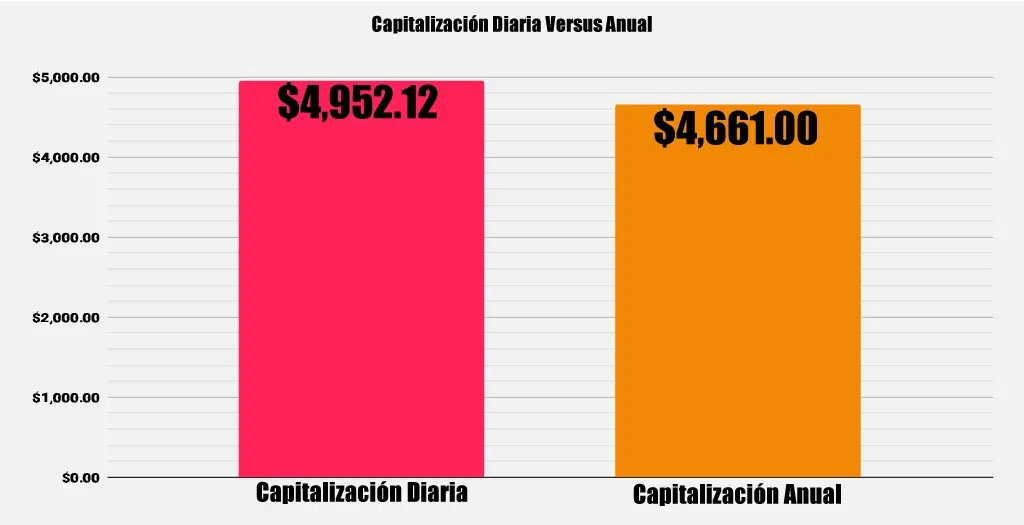
Como puedes ver, cuando la inversión se capitaliza anualmente, se terminó con $4,661.00 en contraste, con $4,952.12 diarios. Ese es el poder de la frecuencia de capitalización.
Ejemplo calcular interés compuesto con contribuciones
Se debe hacer suposiciones para calcular correctamente interés compuesto si agregas depósitos adicionales.
Puedes usar la fórmula en la proxima imagen para calcular cuánto dinero tendrás al final de t años si depositas dinero al comienzo de cada año:

Veamos una ilustración. Considera un escenario en el que tienes $1000 para invertir desde el principio y agregas $100 al comienzo de cada año. Durante tres años, capitalizando mensualmente al 10 por ciento anual.

Importancia de depósitos adicionales
Ahorrar e invertir periódicamente a lo largo del tiempo es clave para acumular ahorros para la jubilación. Una de las mejores técnicas es ahorrar e invertir un porcentaje fijo de tus ingresos. A medida que aumentan tus ingresos a lo largo de tu vida laboral, también lo hace la cantidad que ahorras. Esto puede conducir a una suma sustancial de dinero cuando te retires.
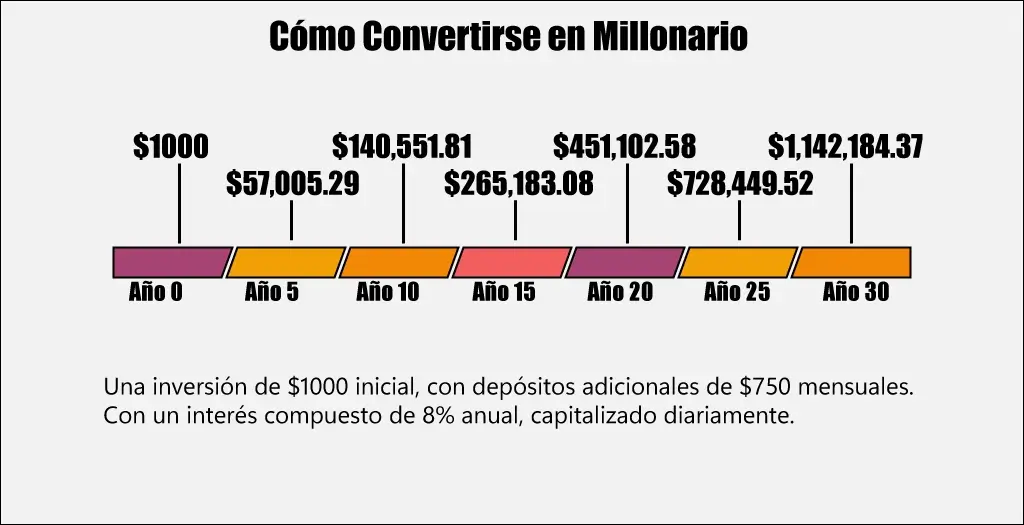
Si comienzas con una inversión inicial de $1,000 y luego aportas $750 cada mes, al interés compuesto al 8% anual, capitalizado diariamente, generarías un balance de más de $700,000 después de 25 años y más de $1,100,000 después de 30 años.


